Lately, I have been reading more papers on modern advances in deep learning in order to get a clear view of what problem I want to focus on during my PhD research.

There is a lot of information to process and an incredible amount of papers are being published from all over the world.

In order to keep up, I will do my best to document everything that I read in this weekly series of paper reviews. The aim is to post one review a week and go from there.

The first paper I will talk about is the one by Chidester, Do, and Ma titled Rotation Equivariance and Invariance in Convolutional Neural Networks.

What is the key problem?

The advantage of convnets over other algorithms is in the amount of different features such network extracts from a given input. Convnets are a very powerful and form a very ubiquitous family of algorithms with various applications in industry.

When it comes to image classification, the same image or the same object in the image could be presented in various positions: it could be shifted left or right, and even rotated. The shift, or, translation, is something the network can withstand. The problem arises when the input is rotated.

If the network has never seen this rotated image, the result of classification will be wrong regardless of whether or not the net has seen the un-rotated original. This originates in the nature of the convolution: the operation of sliding the feature extracting kernel along the image (this is an excellent depiction of convolution).

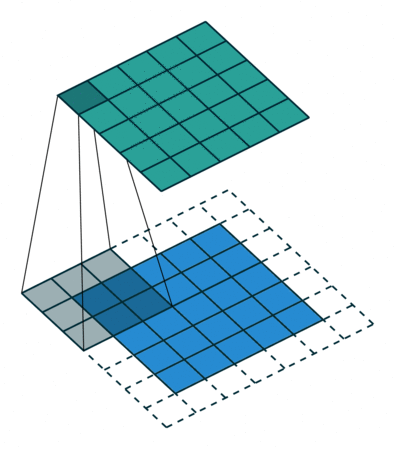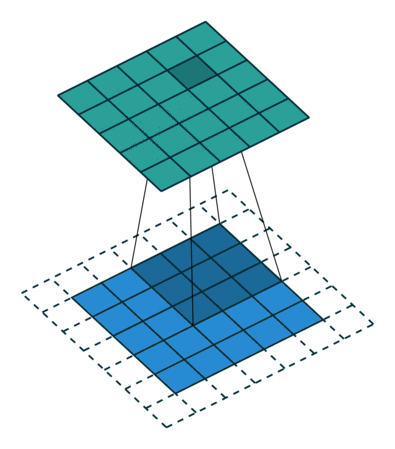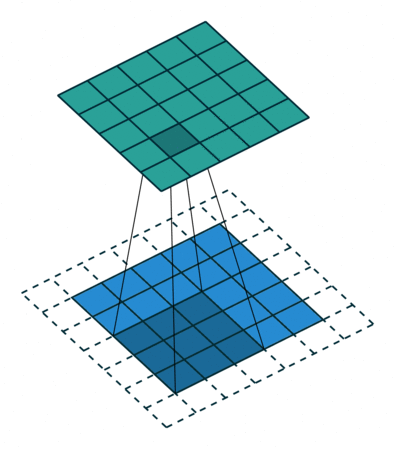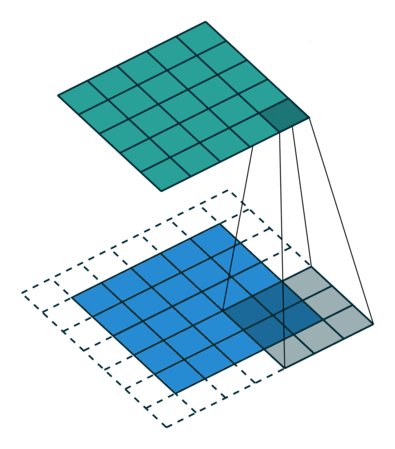Convolution in its natural habitat: a blog post.

One common way of dealing with this is to rotate by a random angle images in the input. This is called augmentation and it increases the number of input data, which in turn may increase training time. Such trade-off is undesirable: why increase training time and sacrifice memory for a super-large network with hundreds of thousands of images already at hand?

Side note: not to say that augmentation is a bad technique. Quite the opposite, it is a very powerful way to avoid overfitting.

So here is the problem: how can the network learn image transformation without explicitly seeing the transformed image during training?

Rotation Equivariance

In the second section of the paper, the authors propose a multi-stage approach to dealing with rotations.

Stage 1 is rotation equivariance, stage 2 is a rotation invariant layer in the network just before the fully-connected classifier block, and stage 3 is the fully-connected layer itself.

Rotation Equivariance

The term equivariance when applied to rotation transformation means the following: if a function acts on an input then the result is. If the input is "corrupted" by a transformation (rotation, shift, etc.), then equivariance with respect to implies existence of a transform such that:

.

The invariance property would look like this:

.

Proposed Solution

Rotation of the Filters

What the authors proposed is to connect rotation of the input with that of the feature extractor explicitly. To elaborate, the convolutional kernel is, essentially, rotated for a desired range of angles. At the same time, the image is split into conic regions, each region will have a designated rotated copy of the convolution kernel. Each rotated kernel is applied to the region.

This formulation opens up a new formalism: a conic convolution.

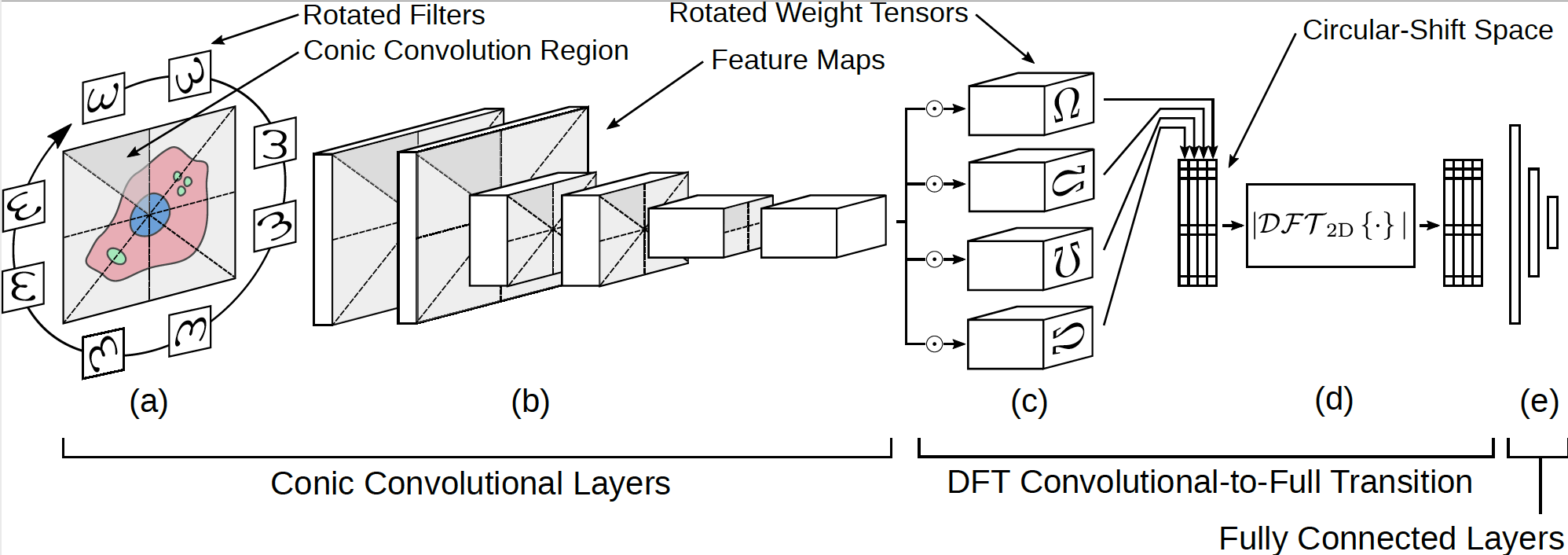Diagram of the proposed network by Chidester, Do, and Ma.

The authors prove a very interesting property of this network. Essentially, the rotation equivariance property we stated still holds, according the results, however, is equal to . (This is proven in Theorem 1 of the article.)

Discrete Fourier transform (DFT)

After that, the results of the conic section of the network need proceed to an additional section before the fully-connected one. It is required to preserve the rotation equivariance extracted by the conic portion before unravelling the tensors.

Such encoding of the equivariance is achieved through the DFT procedure. The authors note the cyclical property of the last convolutional with respect to rotation order. Applying DFT to the output of this convolution yields a representation in which the rotation is "hard-coded".

Finally, this representation is passed into the fully connected layer.

Conclusion

I will not focus this review on the results of the work when applied to benchmark datasets, I believe it is only fair that one refers to the paper itself for that.

Rotation equivariance and general robustness of neural networks to external peturbations is important and in applications such as medical imaging, where the data can be the same image from different angles (or with different transformations applied), a neural network must return a faulty result as the life of a patient is on the line.